Applying Knowledge Distillation to LLMs with Different Vocabularies: the ULD Loss

Large Language Models (LLMs) are powerful tools transforming natural language processing. However, deploying these models in real-world applications is often impractical due to their massive computational costs. Knowledge Distillation (KD) (Hinton et al., 2015) is a transfer learning method that offers a solution by compressing the knowledge from large models (teachers) into smaller, more efficient ones (students). One of the main constraints of this technique comes from the model’s tokenizer, which converts raw text into a structured form called tokens that the model can process. The complete set of tokens used by the model is known as its vocabulary. Traditional knowledge distillation methods typically require the teacher and student models to use the same vocabulary (meaning the same tokenizer). However, this requirement is rarely met, as different model families often rely on their distinct tokenizers.

In our latest paper, Towards Cross-Tokenizer Distillation: The Universal Logit Distillation Loss (Boizard et al., 2024), resulting from our collaboration with the MICS lab of CentralSupelec, we introduced a novel approach enabling effective cross-tokenizer distillation. You can find the code accompanying the paper here. In this blog post, we will explain the key component of the ULD Loss and see why this approach overcomes traditional restriction.

Kullback–Leibler divergence (KLd)

The KL divergence is a way to measure how one probability distribution, let’s call it \( Q(x) \) differs from another probability distribution \( P(x) \).
In the context of knowledge distillation for models, \( P(x) \) represents the probabilities of the tokens predicted by the teacher model, while \( Q(x) \) represents the probabilities of the token predicted by the student model.

Why is it important?

The KL divergence helps the student model to learn by comparing its predictions to the teacher’s predictions. It indicates how “close” the student’s predictions are to the teacher’s, and the goal during training is to minimize the KL divergence as much as possible.

How is it calculated?

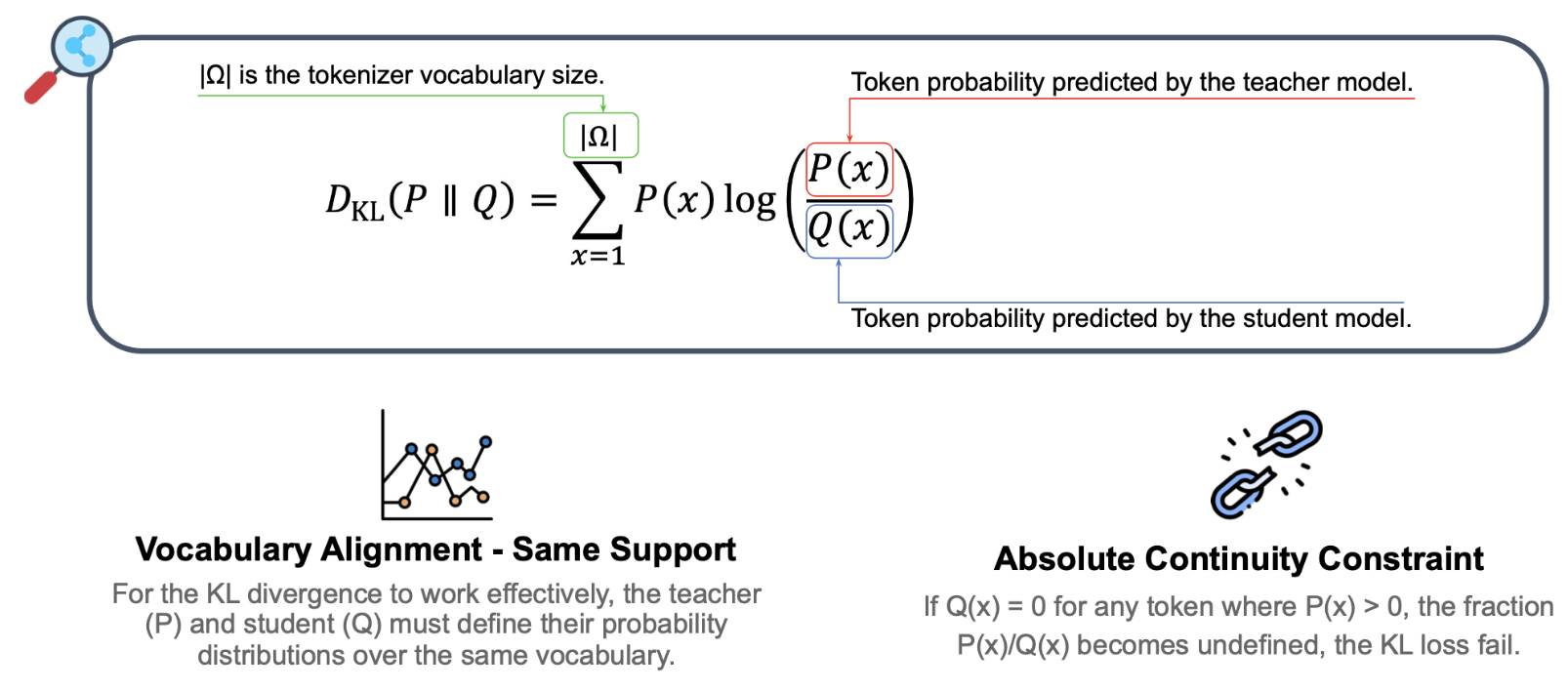
Given the shared vocabulary |\( \Omega \)| , KL divergence is defined as:

\[
D_{KL}(P \parallel Q) = \sum_{x=1}^{|\Omega|} P(x) \log \left( \frac{P(x)}{Q(x)} \right)
\]

Here’s the breakdown of this equation:

• \( P(x) \) : The probability assigned by the teacher.

• \( Q(x) \) : The probability assigned by the student to the same token.

• \( \frac{P(x)}{Q(x)} \) is a ratio used to compare the probability from the teacher to the one from the student for a single token x. The closer its value is to 1, the more similar \( P(x) \) and \( Q(x) \) are.

• \( P(x) \log \left( \frac{P(x)}{Q(x)} \right) \): weights the difference between \( P(x) \) and \( Q(x) \), with \( P(x) \).

The KL divergence is the result of the sum over all tokens in the vocabulary \( \displaystyle \sum_{x=1}^{|\Omega|} \). If the student predicts exactly the same output as the teacher (\( P(x) \) = \( Q(x) \) for all x), the KL divergence would equate 0, this would mean that the student model would behave exactly like the teacher.

Why must the vocabulary be the same?

In the case of transformer models, if two vocabularies are different, say that the student’s vocabulary is {dog, cat, sun} and the teacher’s one {dog, cat, moon}, then the output probability does not exist. In this case \( Q(moon) = 0 \) and \( \frac{P(x)}{Q(x)} \) becomes undefined (division by zero). This breaks the computation and makes the comparison inconsistent.

ULD Loss – Wasserstein distance

We transform our problem into an Optimal Transport problem (OT) and we base our loss function on the  Wasserstein distance which solves this problem, rather than the KL divergence. We call our new method the Universal Logit Distillation (ULD) Loss.

This section focuses on explaining why the Wasserstein distance overcomes the requirement for identical vocabularies between the student and teacher models. For a detailed ablation study, experiments, and results on its impact in knowledge distillation between models with different vocabularies, please refer to our work.

The Wasserstein distance:

The Wasserstein distance is another way to measure the difference between two probability distributions. It is also known as the Earth Mover’s Distance (EMD), and it provides a more geometrically intuitive measure of how much “work” is needed to transform one distribution into another.

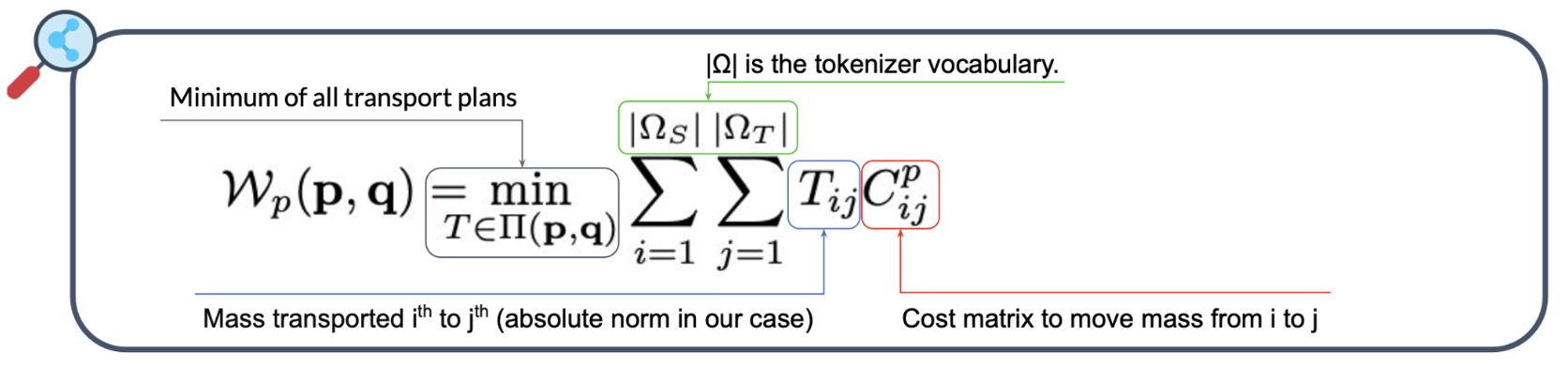
The Wasserstein distance is defined as:

\[
W_p(P, Q) = \min_{T \in \Pi(P, Q)} \sum_{i=1}^{|\Omega_s|} \sum_{j=1}^{|\Omega_t|} T_{ij} C_{ij}^p
\]

Here’s a breakdown of this equation:

• P and \( Q \) are the probability distributions output by the teacher and student, respectively.

• \( T \in \Pi(P, Q) \) is the set of all couplings (joint distributions) between P and \( Q \), meaning that each token in the teacher’s vocabulary is paired with a token in the student’s vocabulary.

• \( C_{ij} \) is the transport cost, which can be seen as the cost to transform \( Q(x) \) in \( P(x) \)

• \(\displaystyle \min_{T \in \Pi(P, Q)} \sum_{i=1}^{|\Omega_s|} \sum_{j=1}^{|\Omega_t|} T_{ij} C_{ij}^{p}\)  finds the coupling set minimizing the cost to transform \( Q(x) \) into \( P(x) \).

Unlike KL divergence, the Wasserstein distance does not require that the vocabularies of the two models P (teacher) and Q (student) match. This is because we are comparing distributions in a more flexible, continuous manner. Each token from P can be mapped to any token in Q, regardless of whether the specific tokens appear in both vocabularies. However, similarly to the KL divergence, the Wasserstein distance value is minimal when (\( P(x) \) = \( Q(x) \) for any x. Therefore, training the student model to reduce this distance, forces the student model to reproduce the behavior of the teacher, or in other words, distills the teacher’s knowledge into the student’s model.

Final thoughts

The ULD loss efficiently distills knowledge between models with different vocabularies (as you can see in our publication). This provides greater flexibility in selecting models for a teacher-student setup, particularly for models trained on different data distributions (different languages for example).